이 글은 머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로의 5장 내용을 기반으로 작성되었다.

차원 축소를 하는 이유는 다양하다. 저장 공간을 줄이고 계산 효율을 높이고, 차원의 저주 문제를 감소시키는 등의 역할을 한다. 또한 중요한 특성만을 추출하여 변환 및 투영을 하면 성능이 올라가는 경우가 많다.

차원 선택이 원본 특성을 중요도에 따라 선택한다면,
차원 추출은 새로운 특성 공간으로 데이터를 변환하거나 투영한다.

5.1 PCA#

PCA는 주성분 분석을 통해서 비지도 데이터를 선형으로 차원 축소하는 기법이다.
PCA는 작은 차원으로 축소시키는 과정이며 이때 주성분을 선택해야 한다. 주성분은 모든 주성분들이 서로 직교한다는(=상관관계가 없다) 가정 하에 가장 큰 분산을 갖도록 선택한다.

5.1.1 PCA 과정#

d차원 -> k차원으로의 PCA의 과정은 다음과 같다.

1. d차원 원본 데이터 표준화
2. 공분산 행렬 생성
   공분산 행렬이란, 두 특성 간의 상관관계를 뜻한다.
   수식은 다음과 같다.
   $\sigma_{jk} = \frac{1}{n-1}\sum_{i=1}^n(x_j^{(i)} - \mu_j)(x_k^{(i)} - \mu_j)$
   여기서 공분산 행렬의 shape은 [d,d]인 square matrix이다.
3. 공분산 행렬을 고유값, 고유벡터로 분해
   고유값은 상수, 고유벡터는 행렬인데 공분산 행렬을 고유값과 고유벡터의 곱으로 나타내는 것이다.
   고유값, 고유벡터에 대한 정의는 복잡하고 재미도 없으니 넘어가자
4. 고유값을 내림차순으로 정렬 후 가장 높은 k개 선택
5. 선택한 k개 고유벡터로 투영행열 W 생성
6. 투영행렬 W를 이용해 원본 데이터를 k차원의 새로운 데이터 차원으로 변환

5.1.2 PCA 구현 코드#

5.1.2.1 직접 구현#

1# 데이터 표준화
2from sklearn.preprocessing import StandardScaler
3
4sc = StandardScaler()
5X_train_std = sc.fit_transform(X_train)
6X_test_std = sc.transform(X_test)
7
8# 공분산 구하고 공분산의 고유값, 고유벡터를 구한다.
9import numpy as np
10cov_mat = np.cov(X_train_std.T)
11eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
12
13# (고윳값, 고유벡터) 튜플의 리스트를 만듭니다
14eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
15               for i in range(len(eigen_vals))]
16               
17# 높은 값에서 낮은 값으로 (고윳값, 고유벡터) 튜플을 정렬합니다
18eigen_pairs.sort(key=lambda k: k[0], reverse=True)
19
20# 여기서는 2개의 특성을 골라서 수평으로 쌓아서 투영행렬 w를 구한다.
21w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
22               eigen_pairs[1][1][:, np.newaxis]))
23               
24# 투영행렬 w를 이용해 pca로 차원축소 시키다.
25X_train_pca = X_train_std.dot(w)

5.1.2.2 사이킷런 구현#

1from sklearn.decomposition import PCA
2
3# 여기서도 데이터를 표준화시켜야 한다.
4# X_train_std는 표준화된 데이터다.
5
6pca = PCA()
7X_train_pca = pca.fit_transform(X_train_std)

PCA( n_componets=[0~1사이의 값] ) 매게변수를 줄 수 있는데 이는 설명된 분산의 비율을 지정해준 값에 맞게 주성분 개수를 선택한다.

여기서 말하는 (설명된 분산 비율) = $\frac{(해당 \,주성분 \, 분산)}{(모든 \,주성분의 \,분산 \,합)}$ 이다.
예를 들어 정렬된 주성분의 설명된 분산 비율이 차례로 0.4, 0.3, 0.2, 0.1 일때
n_components = 0.9이라면 [0.4, 0.3, 0.2]인 주성분을 선택한다.

5.2 LDA#

LDA는 지도 데이터를 선형으로 차원 축소하는 기법이다.

• PCA가 전체 데이터의 분산이 최대가 되도록 주성분을 설정한다고 한다면,
• LDA는 클래스 간 분산(between-class variance)과 클래스 내 분산(within-class variance)을 최대화하고 최소화하려고 노력한다.
  이렇게 하면 서로 다른 클래스 간의 거리가 최대화되며, 같은 클래스 내의 데이터 포인트 간의 거리는 최소화된다.
  

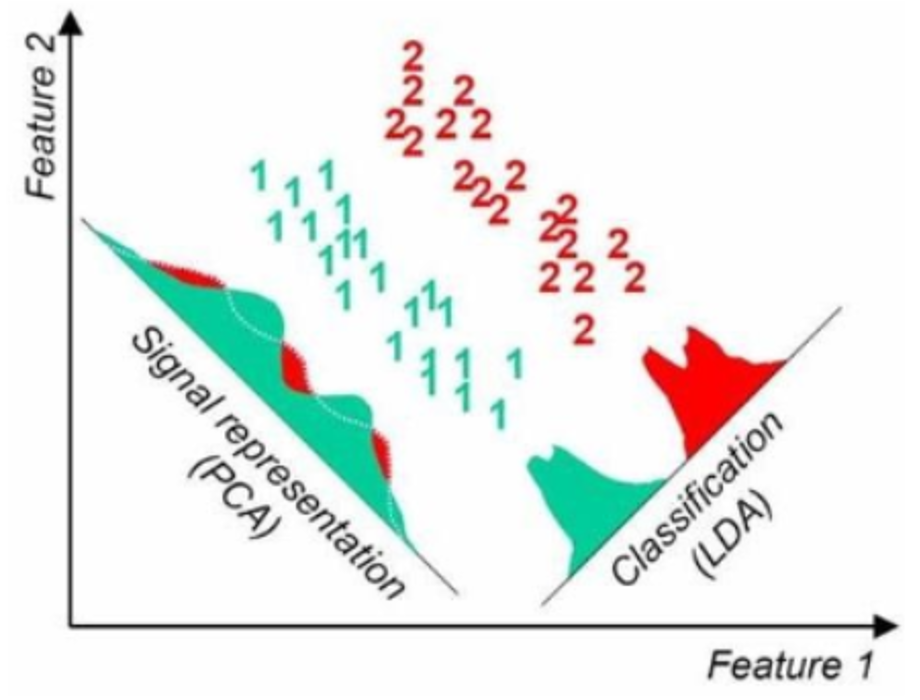
참고로 LDA가 좀 더 분류에 최적화되어 있다고 한다.
그럼 이제 LDA의 과정과 구현을 알아보자.

5.2.1 LDA 과정#

d차원의 원본데이터를 k차원의 데이터로 LDA 차원축소한다고 하자.

1. 원본 데이터 표준화
2. 각 클래스에 대해 d차원의(=특성 d개에 대한) 평균벡터 $m$ 계산
3. 클래스 간 산포행렬 $S_b$와 클래스 내 산포행렬 $S_w$를 계산
   산포행렬이란 데이터들 간의 분산과 공분산을 나타내는다. 이를 통해 데이터 분포를 알 수 있다.
   수식은 다음과 같다.
   $S_i = \sum_{x \in D_i}(x-m_i)^T(x-m_i)$, (여기서 $m_i$는 평균벡터다.)
4. $S_w^{-1}S_b$ 행렬의 고유값, 고유벡터 계산
5. 고유값 내림차순 정렬하여 가장 큰 k개의 고유벡터를 선택
6. 선택한 k개의 고유벡터로 변환 행렬 W 생성
   여기서 W의 각 열이 고유벡터가 된다. 즉 $d \times k$ 차원이다.
7. 변환 행렬 W로 원본 데이터 차원 축소

5.2.2 LDA 구현#

5.2.2.1 직접 구현#

1# 평균 벡터 구하기
2mean_vecs = []
3for label in range(1, 4):
4    mean_vecs.append(np.mean(X_train_std[y_train == label], axis=0))
5    
6# 클래스 내 산포행렬 계산 
7# (row - mv).dot((row - mv).T) 수식을 이용해서 계산했는데,
8# 클래스가 균일하게 분포되어 있지 않을 경우 공분산을 사용하는 게 더 낫다.
9d = 13 # 특성의 수
10S_W = np.zeros((d, d))
11for label, mv in zip(range(1, 4), mean_vecs):
12    class_scatter = np.zeros((d, d))  # 각 클래스에 대한 산포 행렬
13    for row in X_train_std[y_train == label]:
14        row, mv = row.reshape(d, 1), mv.reshape(d, 1)  # 열 벡터를 만듭니다
15        class_scatter += (row - mv).dot((row - mv).T)
16    S_W += class_scatter  
17    
18# 공분산을 이용한 클래스 내 산포행렬 계산
19d = 13  # 특성의 수
20S_W = np.zeros((d, d))
21for label, mv in zip(range(1, 4), mean_vecs):
22    class_scatter = np.cov(X_train_std[y_train == label].T)
23    S_W += class_scatter
24      
25
26# 클래스 간 산포행렬 계산
27mean_overall = np.mean(X_train_std, axis=0)
28mean_overall = mean_overall.reshape(d, 1)  # 열 벡터로 만들기
29d = 13  # 특성 개수
30S_B = np.zeros((d, d))
31for i, mean_vec in enumerate(mean_vecs):
32    n = X_train_std[y_train == i + 1, :].shape[0]
33    mean_vec = mean_vec.reshape(d, 1)  # 열 벡터로 만들기
34    S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)
35
36# 산포행렬의 고유값, 고유벡터 계산
37eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
38
39# 고유값 내림차순으로 정렬
40eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
41               for i in range(len(eigen_vals))]
42eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
43
44# 변환행렬 w 생성
45w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,
46              eigen_pairs[1][1][:, np.newaxis].real))
47              
48# LDA로 차원축소 적용하기
49X_train_lda = X_train_std.dot(w)
50

5.2.2.2 사이킷런 구현#

1from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
2
3# X_train_std는 정규화된 데이터다. 
4# LDA는 정규화를 가정하고 하는 거라 반드시 해주는 것이 좋다.
5
6# n_components LDA로 축소될 차원을 뜻한다.
7# 여기서는 2차원으로 축소했다.
8lda = LDA(n_components=2)
9X_train_lda = lda.fit_transform(X_train_std, y_train)

5.3 커널 PCA (KPCA)#

비선형적으로 분표되어 있는 데이터를 차원축소하기 위해 KPCA를 사용한다.

간단하게 설명하자면,

1. 비선형적으로 분포되어 있는 데이터를 선형적으로 분리할 수 있는 고차원으로 데이터를 투영시킨다.
2. 고차원으로 투영된 데이터를 일반 PCA를 이용해 원하는 작은 차원으로 축소시킨다.

커널 svm과 마찬가지로 이런 방식으로 비선형 데이터 문제를 해결할 수 있다.
다만, 여기서 문제가 고차원으로 투영시키는데 드는 계산 비용이 어마무시하다는 것이다. 이를 해결하기 위해 등장한 것이 **커널 기법(kernel trick)**이다.

5.3.1 커널 기법 (Kernel Trick)#

커널 기법은 흑마법이다. 그니까 증명을 읽었는데도 이해가 안 된다는 얘기다. 흑마법처럼 그냥 받아들이면 편하다.
그래도 최대한 요약해서 이해하기 쉽게 풀어보겠다.

데이터를 고차원으로 투영시키려면 1) 데이터를 고차원 데이터로 변환한 후 2) 변환된 데이터를 내적시켜야 한다. 이 과정에서 어마무시한 계산 비용이 소비된다.
그러나 커널 기법을 사용하면 이렇게 계산을 직접적으로 하지 않고서 같은 결과를 얻을 수 있다.

비유를 하자면, 우리가 1 ~ n 합을 구할 때 1부터 n까지 일일이 다 더해서 구할 수도 있지만 $\frac{n(n+1)}{2}$로 한 번에 계산할 수도 있다. _{아마 이게 커널 기법과 같은 메커니즘이 아닐까 한다.}

여기서 커널 기법을 우리가 직접 구현할 필요가 없고 이미 증명된 커널 기법을 사용하면 된다.

• 다항 커널
• 시그모이드 커널
• 가우시안 커널 (방사 기저 함수, RBF)

5.3.2 KPCA 파이썬으로 직접 구현#

1from scipy.spatial.distance import pdist, squareform
2from numpy import exp
3from scipy.linalg import eigh
4import numpy as np
5
6def rbf_kernel_pca(X, gamma, n_components):
7    """
8    RBF 커널 PCA 구현
9
10    매개변수
11    ------------
12    X: {넘파이 ndarray}, shape = [n_samples, n_features]
13        
14    gamma: float
15      RBF 커널 튜닝 매개변수
16        
17    n_components: int
18      반환할 주성분 개수
19
20    Returns
21    ------------
22     alphas: {넘파이 ndarray}, shape = [n_samples, k_features]
23       투영된 데이터셋
24     
25     lambdas: list
26       고윳값
27
28    """
29    # MxN 차원의 데이터셋에서 샘플 간의 유클리디안 거리의 제곱을 계산합니다.
30    sq_dists = pdist(X, 'sqeuclidean')
31
32    # 샘플 간의 거리를 정방 대칭 행렬로 변환합니다.
33    mat_sq_dists = squareform(sq_dists)
34
35    # 커널 행렬을 계산합니다.
36    K = exp(-gamma * mat_sq_dists)
37
38    # 커널 행렬을 중앙에 맞춥니다.
39    N = K.shape[0]
40    one_n = np.ones((N, N)) / N
41    K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
42
43    # 중앙에 맞춰진 커널 행렬의 고윳값과 고유 벡터를 구합니다.
44    # scipy.linalg.eigh 함수는 오름차순으로 반환합니다.
45    eigvals, eigvecs = eigh(K)
46    eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
47
48    # 최상위 k 개의 고유 벡터를 선택합니다(투영 결과).
49    alphas = np.column_stack([eigvecs[:, i]
50                              for i in range(n_components)])
51
52    # 고유 벡터에 상응하는 고윳값을 선택합니다.
53    lambdas = [eigvals[i] for i in range(n_components)]
54
55    return alphas, lambdas

5.3.2.1 새로운 데이터 포인트 투영#

훈련 데이터셋 외의 다른 데이터셋(훈련 데이터셋, 검증 데이터셋 등)을 모델에 넣을 때 마찬가지로 KPCA 처리하여 투영한 후에 넣어야 한다. 이때 위 코드에서 반환한 고윳값 $\lambda$를 이용하여 KPCA 처리해 준다.
코드는 다음과 같다.

1def project_x(x_new, X, gamma, alphas, lambdas):
2    pair_dist = np.array([np.sum((x_new - row)**2) for row in X])
3    k = np.exp(-gamma * pair_dist)
4    return k.dot(alphas / lambdas)

5.3.3 KPCA 사이킷런 구현#

1from sklearn.decomposition import KernelPCA
2
3# 반달 모양 예시 데이터를 생성한다.
4X, y = make_moons(n_samples=100, random_state=123)
5
6# 사이킷런의 KernelPCA를 수행한다.
7scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
8# 이를 데이터에 적용시킨다.
9X_skernpca = scikit_kpca.fit_transform(X)

요약#

특성 추출을 위한 세 개의 기본적인 차원 축소 기법에 대해서 다뤄봤다. 기본 PCA, LDA, 커널 PCA이다.

• 기본 PCA는 클래스 레이블 없이 직교하는 특성 축을 따라 분산이 최대가 되는 저차원으로 데이터를 투영한다.
• LDA는 클래스 레이블을 사용하여 선형 특성 공간에서 클래스 구분 능력을 최대화한다.
• 커널 PCA는 커널 트릭과 고차원 특성 공간으로의 가상 투영을 통하여 비선형 데이터셋을 저차원으로 극적으로 압축한다. 이를 통해 비선형 데이터를 선형적으로 구분할 수 있게 만든다.