모델이 과대적합이 되었을 때 우리는 norm을 통해 이를 해결한다.
그런데 왜 norm을 사용하는 것이 과대적합을 해결할까? 그 이유를 살펴보자.

과대적합이란 무엇일까?#

모델이 과도하게 훈련 데이터에만 적합되어 있는 것을 뜻한다. 즉, 모델을 일반적인 상황이 아닌 특수 상황에 과도하게 적합된 상태를 뜻한다.

위 그림을 보면 과대적합되면 모델이 너무 복잡해 진다. 즉, 가중치 w 파라미터의 값이 너무 크게 된다는 의미가 된다.

가중치 w가 커지면 결정 경게의 기울기가 증가하고 훈련 데이터 값 하나하나에 더 민감해진다. 따라서 가중치 w가 커지면 모델도 복잡해지는 것이다.
(또한 이는 데이터의 노이즈에도 민감하게 반응하여 모델 복잡성이 높아져도 예측 정확도가 향상되지 안헤 된다.)

어쨌든 그럼 w를 어느 정도 줄여주면 이는 모델의 복잡도의 감소로 이어진다. 이런 방법을 normalization 즉, 규제(표준화)라고 한다.

여기서 잠깐, 분산과 편향이란 무엇일까?#

다음 사진을 보면 이를 잘 이해할 수 있다.

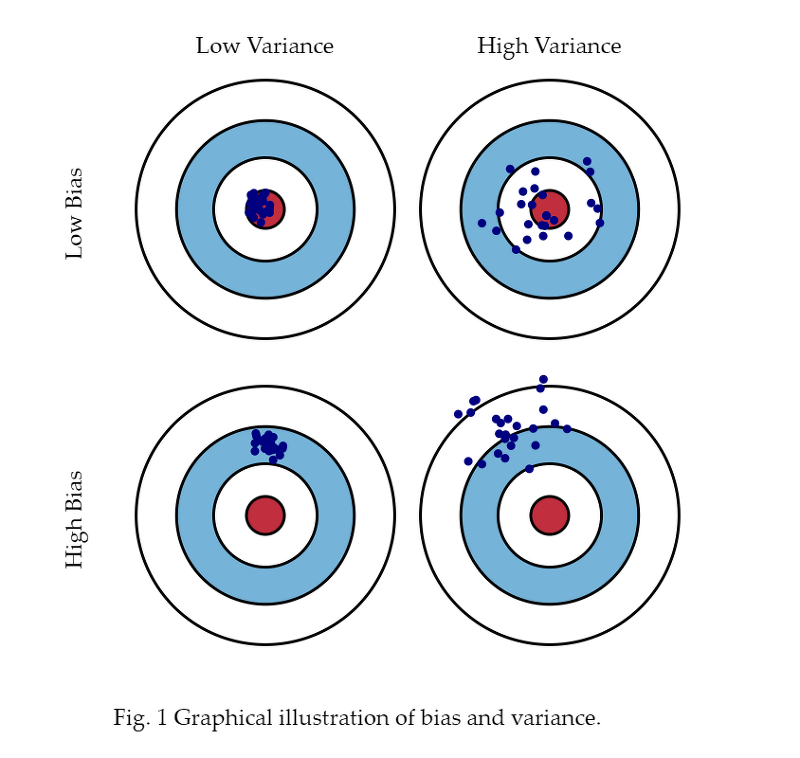
그럼 다음 사진은 분산이 작고, 편향이 크다... 하하

L2 Norm#

자주 쓰는 norm 기법으로 L2 norm이 있다. (L1 norm도 있긴 한데 넘어가자)

여기서 $\lambda$는 norm의 하이퍼파라미터이다.
이를 비용함수에 norm 항을 추가시킨다.

이렇게 되면 w값이 크면 비용함수 또한 커지기 때문에 자연스럽게 w의 값이 줄어들고 이는 곧 모델의 복잡도 감소로 이어진다.
따라서 L2 norm이 과대적합 문제의 해결방안이 된다.

그럼 과소적합은 뭘까?#

편향이 클 때를 과소적합이라고 한다. 모델이 너무 단순하여 훈련데이터를 충분히 설명하지 못 한다.
즉, 모델의 결정 경계에서 멀리 떨어져 있게 된다. 이는 편향이 큰 것으로 이어진다.
그럼 이를 해결하려면 어떻게 할까?

과소적합 해결 방법#

단순히 과대적합의 해결방안을 반대로 하면 해결된다. 과대적합과는 반대로 모델의 복잡도가 너무 낮아서 나타나는 현상이니 이를 높여주면 해결되는 것이다.

• 규제 풀기
  규제로 인해 가중치 w가 낮다면 $\lambda$를 감소시켜서 규제를 완화시킨다. ($\lambda$가 크면 강한 규제, $\lambda$가 낮으면 약한 규제이다)
• 모델 복잡성 증가
  더 많은 파라미터를 추가하거나 더 복잡한 알고리즘을 선택할 수 있다. 대표적인 예시로는 다항 회귀 모델이 있다.
  다항 회귀 모델이란 다음과 같다.
  
• 더 많은 데이터 수집
  과소적합은 데이터 부족으로 인해서도 나타날 수 있다. 더 많은 훈련 데이터를 제공하면 모델은 더 일반화된 경향 즉 복잡도가 높아질 것이다.

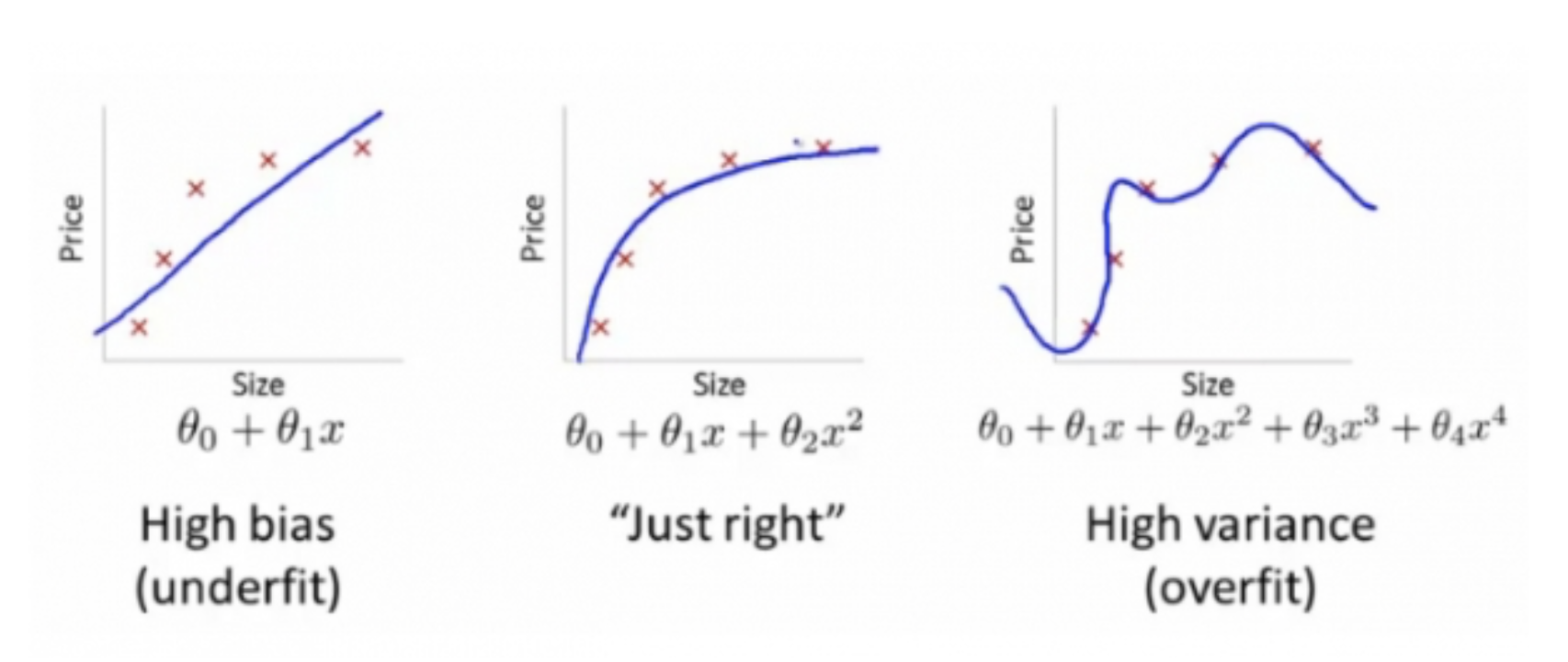
이상으로 과대적합과 과소적합, 그리고 norm에 대해서 살펴보았다.