Transformers
Seq2Seq에서 RNN을 아예 빼버리고 attention으로 구성해보면 어떨까? → Transformer의 구조 현재는 seq2seq + attention에서는 하나의 벡터로…
2025/04/27
Jinsoolve.
레이블이 없는 데이터들을 분석하여 비슷한 데이터들끼리 그룹으로 묶을 것이다.
이를 군집으로 묶는다하여 클러스터링(clustering)이라 한다.
k-평균 알고리즘은 단순하고 쉽다는 장점이 있지만 그룹의 개수를 정하는 k의 값에 따라 성능이 말도 안되게 달라지고 데이터가 고차원일수록 이 k값을 찾기가 어렵다.
그룹의 대표하는 값을 프로토타입이라고 하는데 연속현 데이터에서는 평균(센트로이드)을 사용하고 범주형 데이터에서는 가장 대표되는 값이나 자주 등장하는 값(메도이드)으로 사용한다.
이 k값에 대한 성능을 평가하는 엘보우 방법이나 실루엣 그래프라는 것이 있다.
k-평균의 초기 센트로이드를 정할 때 똑똑하게 할당하지 못하면 (빈 클러스터가 생겨나거나 한다) 성능이 나빠지거나 수렴이 느려진다. 이를 똑똑하게 할당하기 위해서 k-평균++알고리즘을 이용한다.
초기 센트로이드가 서로 멀리 떨어지도록 위치한다.
초기 센트로이드를 랜덤하게 고르고 골라지지 않은 샘플들과의 거리를 이용하여 제대로된 센트로이드를 선택하도록 한다.
한 개의 샘플이 하나의 클러스터에만 포함되어 있으면 직접군집,
한 개의 샘플이 여러 개의 클러스터에 속할 수 있으면 간접군집이라 한다.
간접군집의 대표적인 예시가 퍼지 k-평균으로, FCM 알고리즘이라고 불린다.
샘플이 각 클러스터에 속할 확률값을 이용하여 해당 값이 더는 최적화되기 전까지 최적화시킨다. 클러스터 속할 확률을 계산하는데 비용이 들지만 최적화 수렴할 때까지 반복 횟수가 적게 들기 때문에 k-평균과 비슷한 결과를 만든다.
k-평균 알고리즘을 평가 지표를 이용해 k값을 최적화 시키는 방법이 있다.
기본적인 성능 계산방법은 SSE(Sum of Squared Errors) 즉, 오차 제곱의 합을 통해서 계산한다. 이때 엘보우 방법은 k값에 따른 SSE의 값을 그래프로 그려봤을 때 급감하는 지점을 찾는 것이다.
클러스터 내부의 점끼리의 거리 지표인 응집력과
다른 클러스터 간의 거리 지표인 분리도를 이용한다.
응집력과 분리도의 차이를 둘 중 큰 값으로 나눈 것이 실루엣 계수 값이다. -1과 1 사이의 값을 갖는다.
즉 응집력과 분리도가 비슷할수록 실루엣은 0에 가까워지고, 차이가 커지면 1에 가깝게 된다. 분리도는 클러스터간 분리가 얼마나 잘 되어 있는지를 나타내고 응집력은 클러스터안이 얼마나 잘 뭉쳐있는지를 나타내기 때문이다.
따라서 실루엣 계수가 0에서 멀리 떨어질수록 좋은 결과로 해석할 수 있다.
클러스터 계수를 일부로 잘못 설정한 예시를 보자.
위의 결과는 좋지 않은 것처럼 보이지만 클러스터 2개로 할 수 있는 나름의 최선을 한 결과이다.
계층 군집에는 병합 계층 군집과 분할 계층 군집이 있다.
여기서는 병합 계층 군집��을 자세히 다루겠다.
기본적으로 클러스터 간 거리가 짧은 클러스터부터 합치는데
클러스터 간의 거리를 정의하는 방식이 2가지가 있다.
사이킷런에 AgglomerativeClustering 클래스가 구현되어 있다.

k평균 알고리즘이나 계층 알고리즘이 원형으로 모양을 가정한 후에 클러스터링을 했다면 DBSCAN은 밀집도를 기반으로 비교적 자유로운 모형을 만든다.
즉, 많이 모여있으면 무슨 모양이든지 해당 부분을 클러스터링한다.
모양이 자유롭고 모든 샘플을 클러스터에 할당하지 않고 잡음 샘플을 구분한다.
위 그림과 같은 반달 모양의 데이터가 있다고 하자.
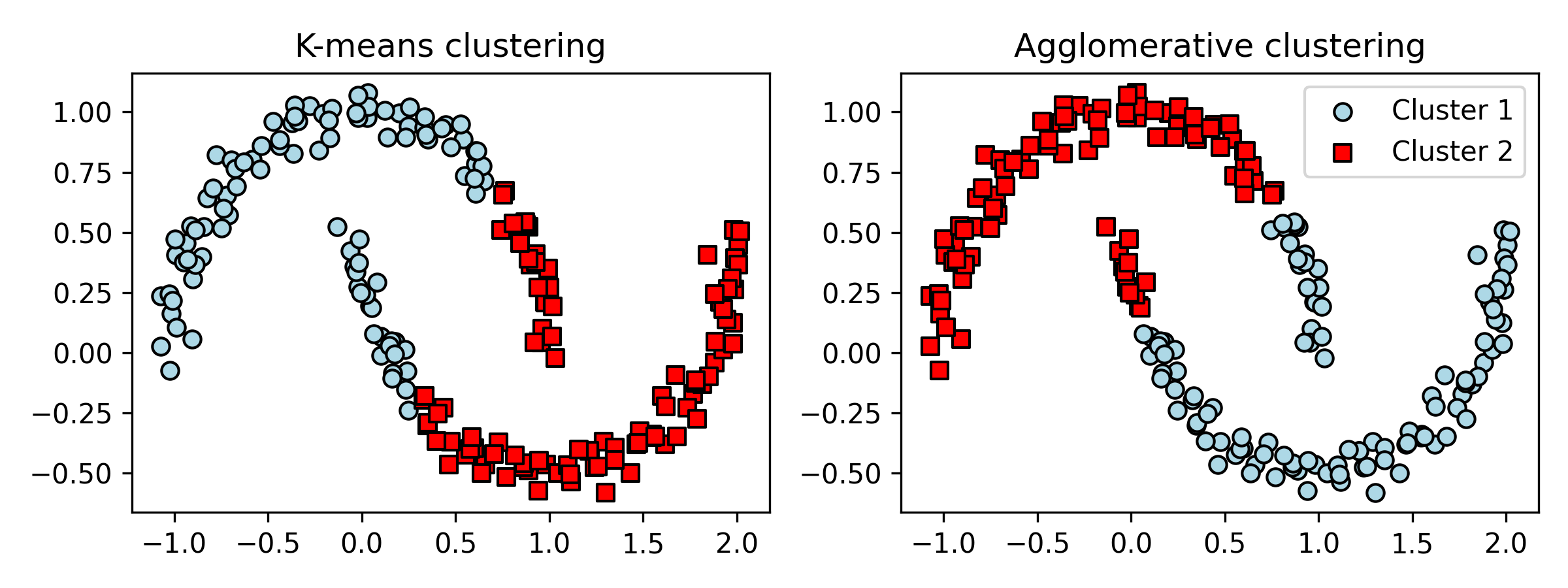
왼쪽은 k평균, 오른쪽은 계층 알고리즘�이다.
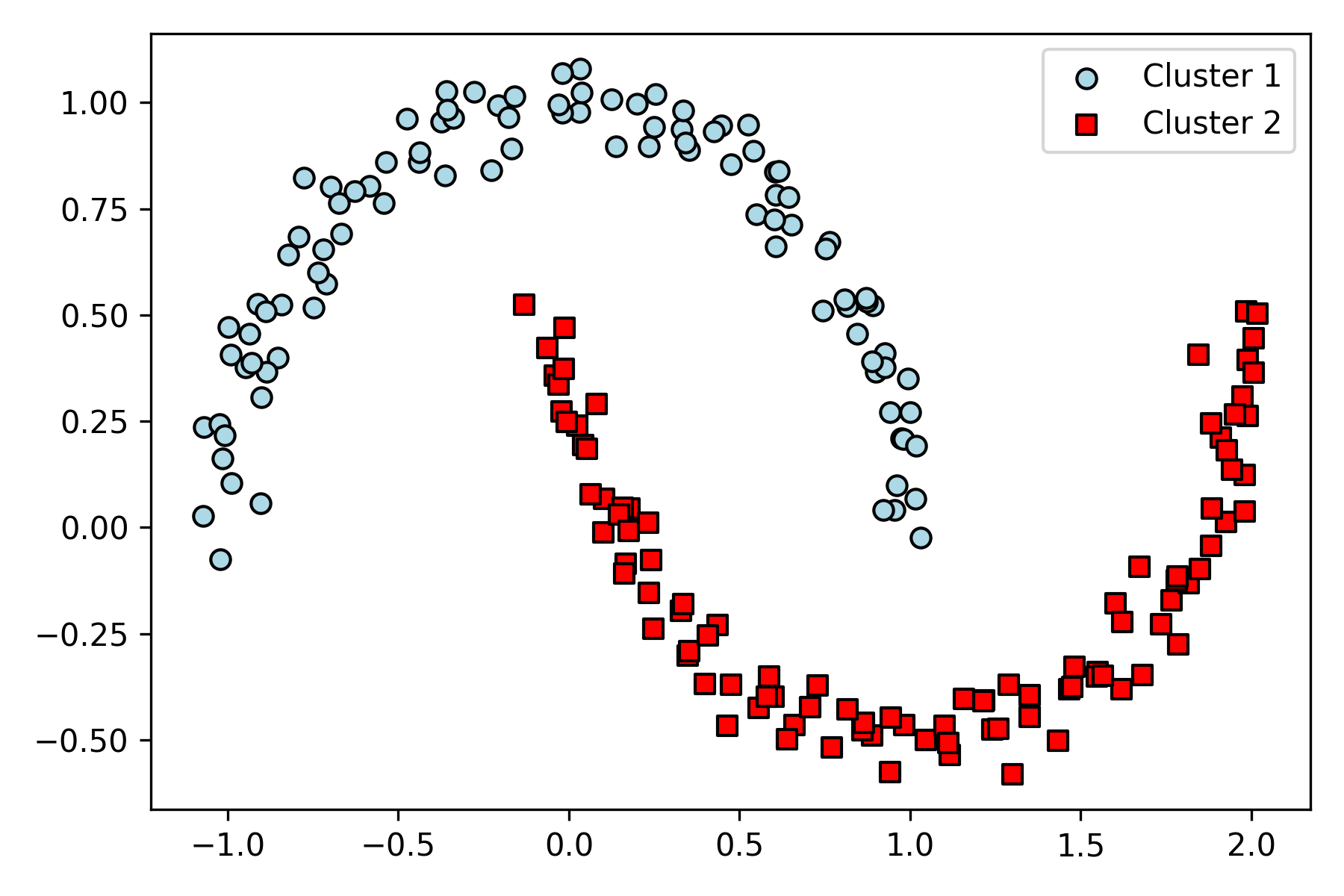
반면 DBSCAN 은 잘 잡아낸다.
하지만 특성 개수가 늘어나면 여전히 차원의 저주로 인해 역효과 증가. (이건 k-평균과 계층군집도 마찬가지)
또한 두개의 하이퍼파라미터(Minpts와 )을 최적화시켜야 한다.
프로토타입 기반 군집인 k-평균, 병합 계층 군집, 밀집도 기반군집(DBSCAN)을 살펴보았다.
그래프 기반 군집인 스펙트럴 군집 또한 소개하겠다.
유사도 행렬 또는 거리 행렬의 고유 벡터를 사용하여 클러스터 관계를 유도한다.
Seq2Seq에서 RNN을 아예 빼버리고 attention으로 구성해보면 어떨까? → Transformer의 구조 현재는 seq2seq + attention에서는 하나의 벡터로…
2025/04/27
성# Language Model(LM)이란? 언어 모델이라는 건, 사실 다음에 올 단어를 확률로 예측하는 것이다. 이러한 언어 모델들을 어떻게 발전시켜왔는 지 살펴보자. 이미 이…
2025/04/27
이전 포스트에서 RNN에서 Vanishing Gradient로 인해 장기 의존성 문제가 있다는 사실을 이야기했다. 이런 Vanishing Gradient를 해결하기 위해 크게…
2025/04/27
기존 RNN의 병목 현상을 해결하기 위해 Attention이 등장했다. Decoder에서 한 단어를 예상할 때, 해당 단어와 특별히 관련되어 있는 Encoder의 특정 단어를…
2025/04/27