머신러닝 교과서 10장

선형 회귀 모델에 대해 알아보자.

보스턴 집 가격 예측 문제를 예시로 들어서 설명하겠다.

---

데이터 셋을 상관관계나 산점도를 그려 분석한다.

---

사이킷런의 LinearRegression()을 사용해 모델링한다.
경사하강법으로 모델의 파라미터 최적화를 시킨다.

---

선형 회귀 모델은 이상치에 영향을 많이 받기 때문에 이상치를 제거하는 것이 좋다. 이상치를 감지하는데 사용할 수 있는 통계적 테스트가 많지만 이번에는 제거하는 방식 대신 RANSAC(RANdom SAmple Consensus) 알고리즘을 사용하겠다.

RANSAC을 통해 이상치의 잠재적인 영향을 감소시킨다.

---

선형 회귀 모델의 성능을 평가하는데 차이 혹은 차이^2을 이용한다.
이때 차이값을 비교하기 위해서는 표준화해야 한다.

$R^2$ 지표도 사용한다. 평균제곱오차(MSE)와의 차이는 다음과 같다.

---

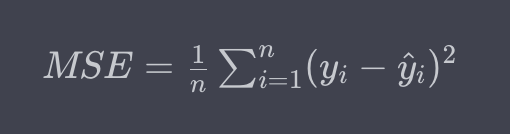
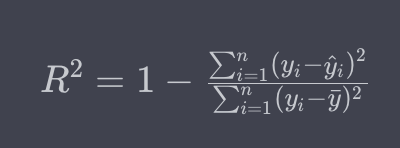
과대적합을 방지하기 위해 규제를 사용한다.

---

선형 회귀 모델을 다항 회귀로 변환 -> 비선형도 가능해진다
PolynomialFeatures를 이용하여 feature들을 추가한다.
2차, 3차 등의 다항식을 추가시켜 모델을 학습시킨다.

다항 특성을 많이 추가할수록 모델의 복잡도가 높아지고 과대적합할 가능성이 높아진다.

다항 특성이 비선형 관계를 모델링하는데 언제나 최선의 선택인 것은 아니다. 두 변수의 관계가 지수함수와 유사하다면 로그 변환을 해줄수 있다.

---

랜덤 포레스트를 사용하여 비선형 관계 다루기

결정트리 회귀는 특성 변환이 필요하지 않다. 한 번에 하나의 특성만 고려하기 때문이다. 결정트리는 일반적인 경향을 잘 잡아내지만 예측이 불연속적이고 매끄럽지 못하다.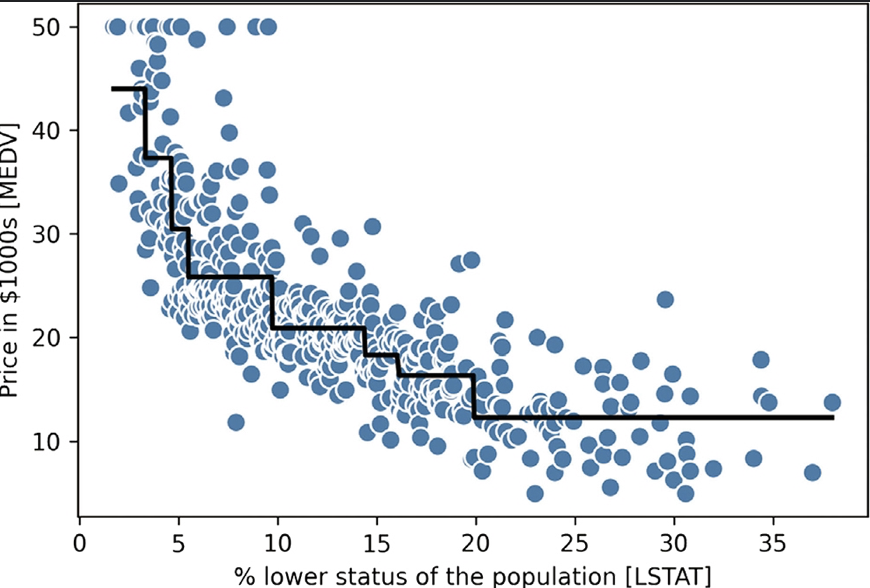

이를 랜덤포레스트를 활용하면 어느 정도 해결할 수 있다. 더 좋은 일반화성능을 가지며 분산을 낮춰준다. 앙상블 트리 개수가 랜덤포레스트의 유일한 하이퍼파리미터인 것이 장점이다.

잔차 그래프(residual plots)의 분포가 랜덤하지 않는다면(어느정도 규칙성을 띄고 있다면) 모델이 특성의 정보를 제대로 잡아내고 있지 못 한것이다. 그러나 단일 결정트리보다는 여전히 좋은 성능을 내고 있다.

SVM 회귀
커널 SVM으로 비선형 회귀문제를 해결할 수 있다. 사이킷런에 구현되어 있으니 참고하면 좋다.