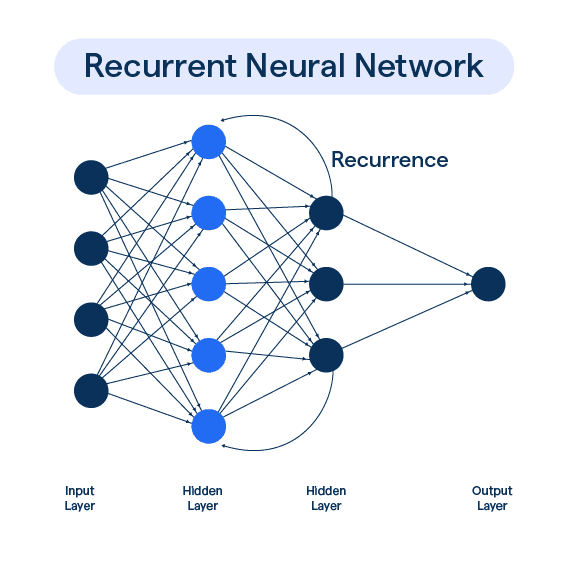
Transformers
Seq2Seq에서 RNN을 아예 빼버리고 attention으로 구성해보면 어떨까? → Transformer의 구조 현재는 seq2seq + attention에서는 하나의 벡터로…
2025/04/27
Jinsoolve.
Created At: 2024/12/26
1 min read
Locales:
ko
en
The cost function of logistic regression is as follows:
Why does the cost function look like this?
To understand this, we first need to understand the concept of log-odds.
In linear regression, the prediction values range from to .
In logistic regression, however, there is a key difference: instead of predicting a value directly, it calculates a log-odd.
However, since the odds range from [0, ] and are asymmetric, they are difficult to use as-is.
To address this, a log function is applied as follows:
However, Logit still has a range of [, ], which makes it unsuitable for direct use as probabilities.
The sigmoid function is used to map the range to [0, 1], making it suitable for representing probabilities.
Let , then:
The sigmoid function helps transform the logit into a probability range. For better understanding, let’s illustrate this with a graph:
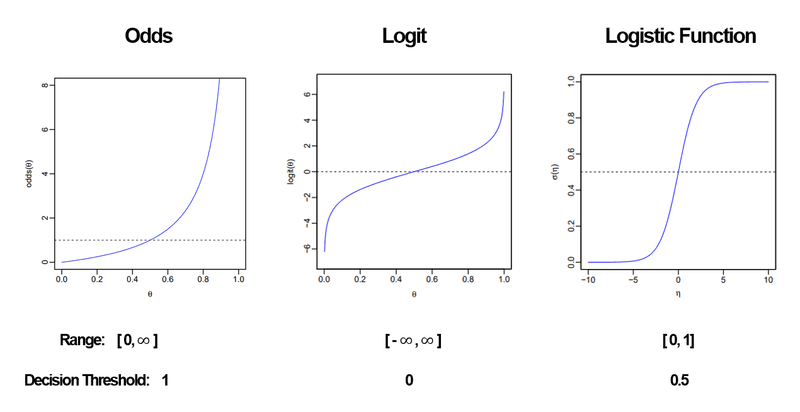
This process leads to the well-known sigmoid function graph.
Now, we have some understanding of what means.
But what does represent?
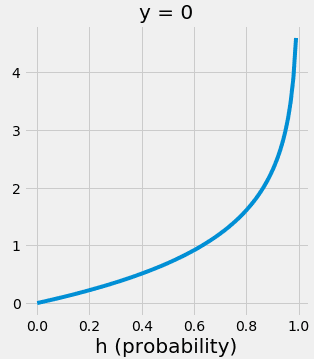
Let’s plot the graph of (with log = ln):
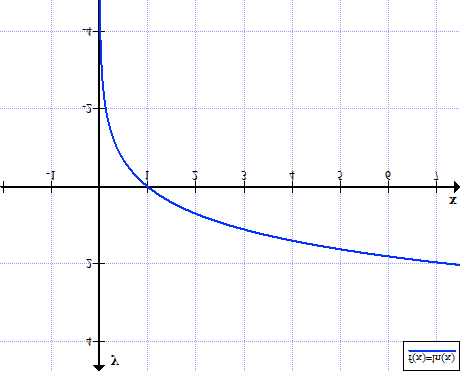
Since ranges from [0, 1], it looks like this:
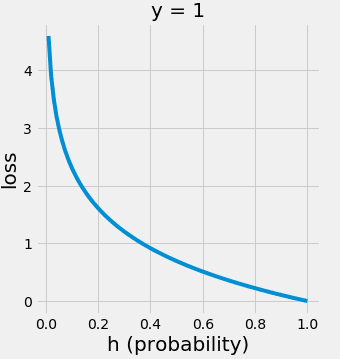
The closer the prediction is to 1, the smaller the value of . Conversely, the further the prediction is from 1, the larger the value.
In other words, this represents a loss function: the worse the prediction, the higher the loss.
(Note that the cost function is the average of the loss functions across the entire dataset.)
Similarly, can be considered the loss function when predicting 0.
Thus, for all m data samples:
When a sample belongs to class 1, add .
When a sample belongs to class 0, add .
This gives the total loss value.
Hence, the following equation holds:
Seq2Seq에서 RNN을 아예 빼버리고 attention으로 구성해보면 어떨까? → Transformer의 구조 현재는 seq2seq + attention에서는 하나의 벡터로…
2025/04/27
성# Language Model(LM)이란? 언어 모델이라는 건, 사실 다음에 올 단어를 확률로 예측하는 것이다. 이러한 언어 모델들을 어떻게 발전시켜왔는 지 살펴보자. 이미 이…
2025/04/27
이전 포스트에서 RNN에서 Vanishing Gradient로 인해 장기 의존성 문제가 있다는 사실을 이야기했다. 이런 Vanishing Gradient를 해결하기 위해 크게…
2025/04/27
기존 RNN의 병목 현상을 해결하기 위해 Attention이 등장했다. Decoder에서 한 단어를 예상할 때, 해당 단어와 특별히 관련되어 있는 Encoder의 특정 단어를…
2025/04/27